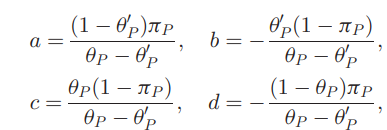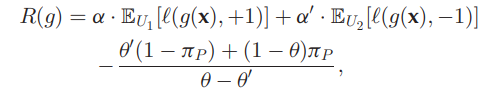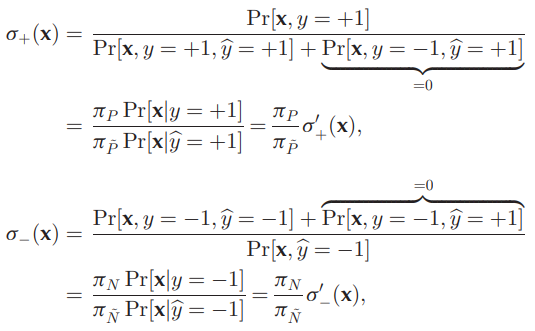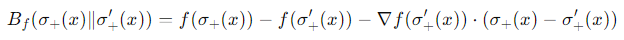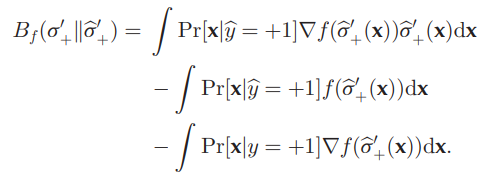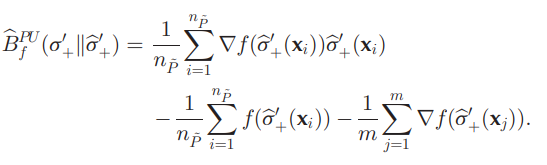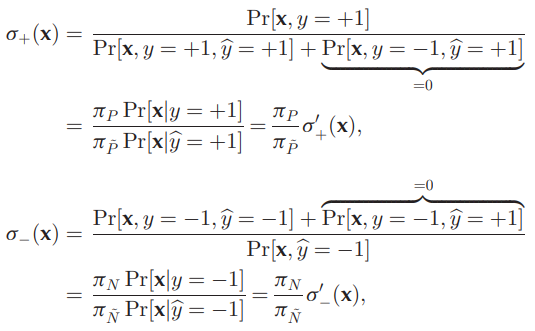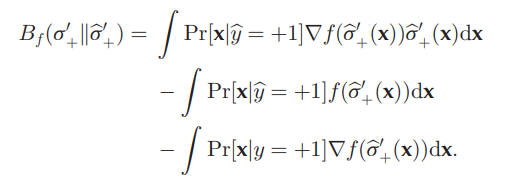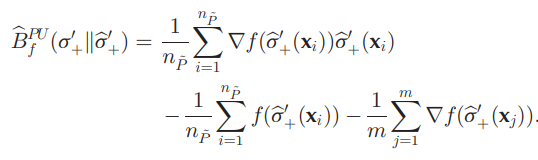Sen(Qian)’s Memo

https://ieeexplore.ieee.org/document/9361098

2019年にeもKDDに出している。

この論文は以下の3点の貢献がある。

1. PU Learningしていくときに、時たま出るおかしな予測について、学習アルゴリズムの「ノイズ」のせいだとしている。そして、それを補正していきたい。
2. それについての、超過リスク分析？に基づく新しい手法を提案した。
3. 実験で正しさを証明した。

📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future

📄2020-Survey-Learning from positive and unlabeled data: a survey

Semi-supervised Learningベースの手法もあるらしい。

Importance Weightingベースの方法あるらしい。

UU Learningベースの手法もあるらしい。

• サンプルは$\mathbf{x} \in X$、ラベルは$y \in \{-1, +1\}$で、+1がP、-1がNデータ。
• PUなので、実際には$y$は与えられず、Pは必ずPだがUはPかNかはわからないという設定。
• PUの式は以下の2つである。数学的には等価であるが、下の方がよくつかわれる。

• UU Learningは2つのUnlabeledの分布があり、それぞれClass Priorが$\pi_1, \pi_2$であるとき、以下の式の最小化になる。
  • まずU1について、lossの合計は係数$a, b$を使って$a l(\cdot, +1) + b l(\cdot, -1)$として、U2についても同様に$c l(\cdot, +1) + d l(\cdot, -1)$としている。
  • この時、これらを用いて$a \pi_1 + d\pi_2 = \pi_P, b (1 - \pi_1) + c(1 - \pi_2) = \pi_N$であるとあらわせる。
  • この時、以下のような式でUU Learningできる。

  

  

• 問題設定は、以下のようなノイズ。
  • 与えられるのはPUのデータセット。
  • Pデータは完ぺきにPで構成されている。
  • Uデータはいつも通りPとUによって、Class Prior$\pi$の混合比である。
  • ノイズとは、PU Learningしたときに、時たま明らかにおかしい予測をしてしまう問題を指す。なので、これは「学習アルゴリズム」や「各データ」に依存して起きる。
  • これをうまく較正していくのが目標。

PU Learningを用いて、分類器$g_{PU}$を訓練し、U Dataにそれを用いてPseudo Labelをつけていく。

UにPseudo Labelが付与されたら、Pseudo LabelがPのものの集合は$Q_P$、Nのものは$Q_N$とする。

Uに対するPseudo Labelが完全に正しいというわけはないので、これをできるだけ是正していきたいと考える。

ここで、下図のようなもともとの$\sigma_+. \sigma_-$を式変形と$\pi_P \approx \pi_{\bar{P}}, \pi_N \approx \pi_{\bar{N}}$の前提をおいて、$\sigma_+^\prime, \sigma_-^\prime$を代わりに推定しそれで$\sigma_+$などを代替する。

$\sigma_+^\prime(\mathbf{x})$は与えられたPデータにより$p(\mathbf{x}|y=+1)$は経験分布として既知で、Pseudo LabelのPとなっているものにより、$\hat{p}(\mathbf{x}|y=+1)$を推定する。

$\sigma(\mathbf{x})$は与えられたPデータで同様に$p(\mathbf{x}|y=+1)$は経験分布として既知で、$p(\mathbf{x}|y=+1)$はわからない。

本来これについてモデルを当てはめたいところだが、次でいうBregman Divergenceの計算でそれは実は不要とわかる。

Bregman Divergenceの定義として、微分可能な$f$な凸関数を使う、Bregman Divergence$D_f$は以下のようになる。

例えば、$f(x) = ||x||^2$となるとき、これは$||x||^2- ||y||^2- \langle 2y, x-y \rangle = 2 ||x-y||^2$となり、ユークリッド距離になるらしい。

これを今回は、ある関数$f$によって、$D_f(\sigma_+||\sigma_+^\prime)$を計算する。分布についてのBregman Divergenceは、このように全体を積分していく(期待値

ここでは、以下のようにBregman Divergenceはなるらしい。

これを経験的に解くと、以下の式になる。

これを計算することにより、$\sigma_+$の$p(\mathbf{x}|\hat{y}=+1)$の値を明確に推定せずとも、$\sigma_+$の推定値がわかる。

1つ目の損失はPseudo Labelについて。

仮定により、与えられるPは完ぺきにCleanなので、$Q_P$は$P$データと同じ分布に従うはず。だからこの2つの経験分布は距離が最小ひいては0でなければならない。

だが、学習アルゴリズムやデータに依存するNoiseというのがあるため、ここの差異を是正しないといけない。これの一環として、$\sigma_+, \sigma_-$を推定して、補正を掛ける。

以上のように、定義で0になっている部分を足してあげることで、新たな式変形$\sigma^\prime_+$などができる。

ここで$\pi_P/\pi_{ \bar{P}}$などがあるが、実際の推定はこの部分は大体1だとして、直接$\sigma_+^\prime(\mathbf{x}) = Pr(\mathbf{x}|y=+1)/Pr(\mathbf{x}|\hat{y}=+1)$などを推定し、これを$\sigma_+(\mathbf{x})$と等しくなるべきだろう、と考える。

その尺度として、Bregman Divergenceを使っている。

定義として、微分可能な$f$な凸関数を使う、Bregman Divergence$D_f$は以下のようになる。

例えば、$f(x) = ||x||^2$となるとき、これは$||x||^2- ||y||^2- \langle 2y, x-y \rangle = 2 ||x-y||^2$となり、ユークリッド距離になるらしい。

$\sigma_+(\mathbf{x}) = p(\mathbf{x}|y=+1)/p(\mathbf{x}|\hat{y}=+1)$である。与えられているPデータは絶対に正しい$p(\mathbf{x}|y=+1)$の経験分布ので、動かす必要があるのは$p(\mathbf{x}|\hat{y}=+1)$だけ。

以下のように、推定したい$\sigma_+$と$\sigma_+^\prime$の間でBregman Divergenceを考え、最小化するように$\sigma_+$を動かしていく。

我々はPU Learningの識別器から、Uの中にあるPseudo LabelがPであるデータに

これと似てるように、$\sigma_-$の予測はできる。